Research at the Laboratory of Crystallography

The structure of the Charge-Density Wave in (TaSe₄)₂I

(TaSe₄)₂I is a quasi-1-dimensional (1D) metal, that belongs to the class of (MX₄)xY compounds (M = Ta, Nb; X = S, Se, Te; Y = I, Br, Cl; x>= 2). Characteristic feature of these compounds are the columns of composition MX₄ that are separated by chains of halogenide atoms. (TaSe₄)₂I crystallizes in the tetragonal space group I422 with lattice parameters a₀ = b₀= 9.531 Å and c₀= 12.824 Å at room temperature (Figs. 1 and 2). The 1D electronic properties are presumably related to the 1D electron band formed by the 5d_z² orbitals of the Ta atoms.

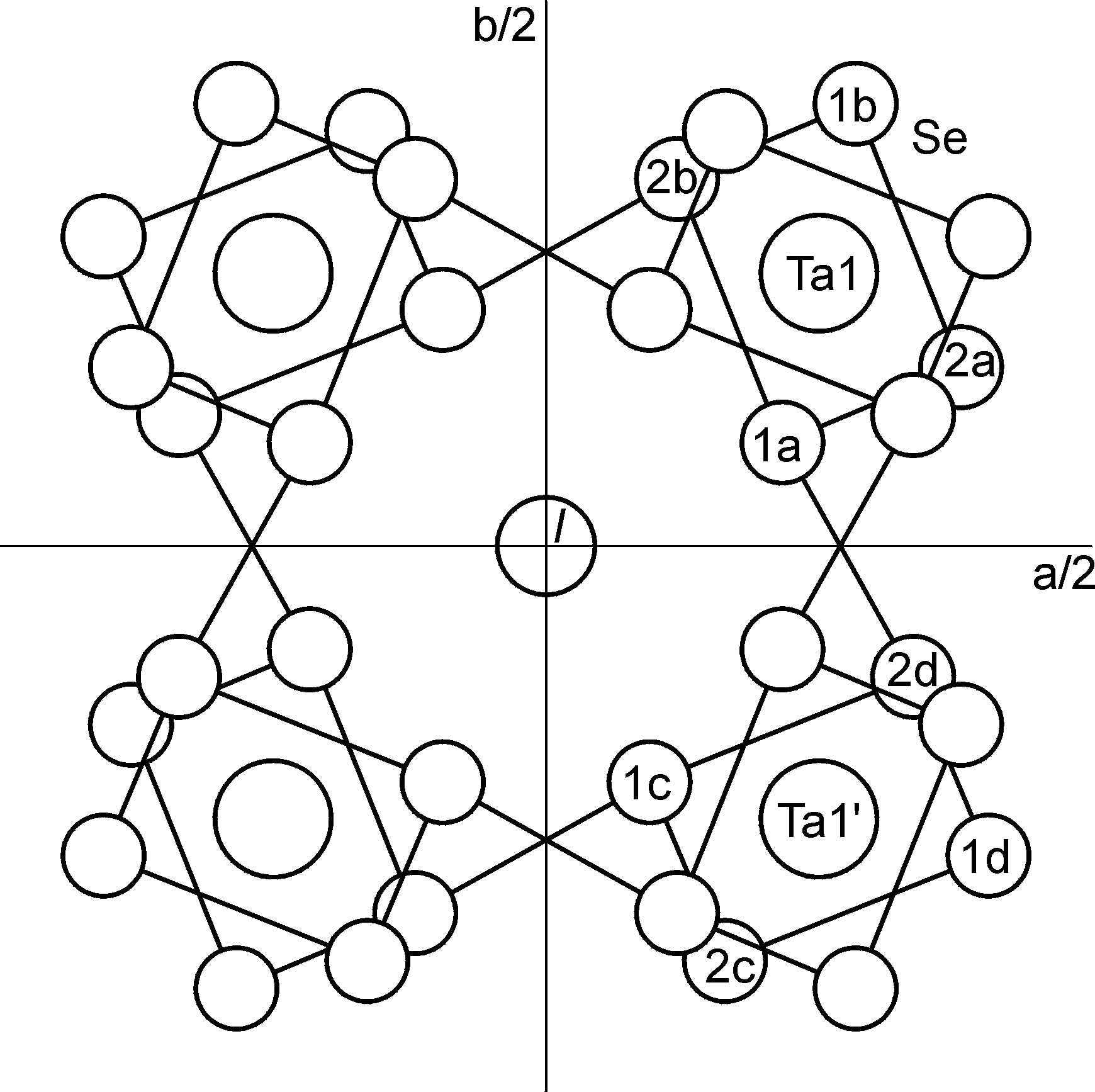
Fig.1: Projection of the basic structure of one unit cell onto the a, b- plane. Shown are Ta1 atoms at z = 0, iodine atoms at z = 0.15, Se atoms at z~-0.12 (indicated by the numbers), and Se atoms at z~ 0.12.

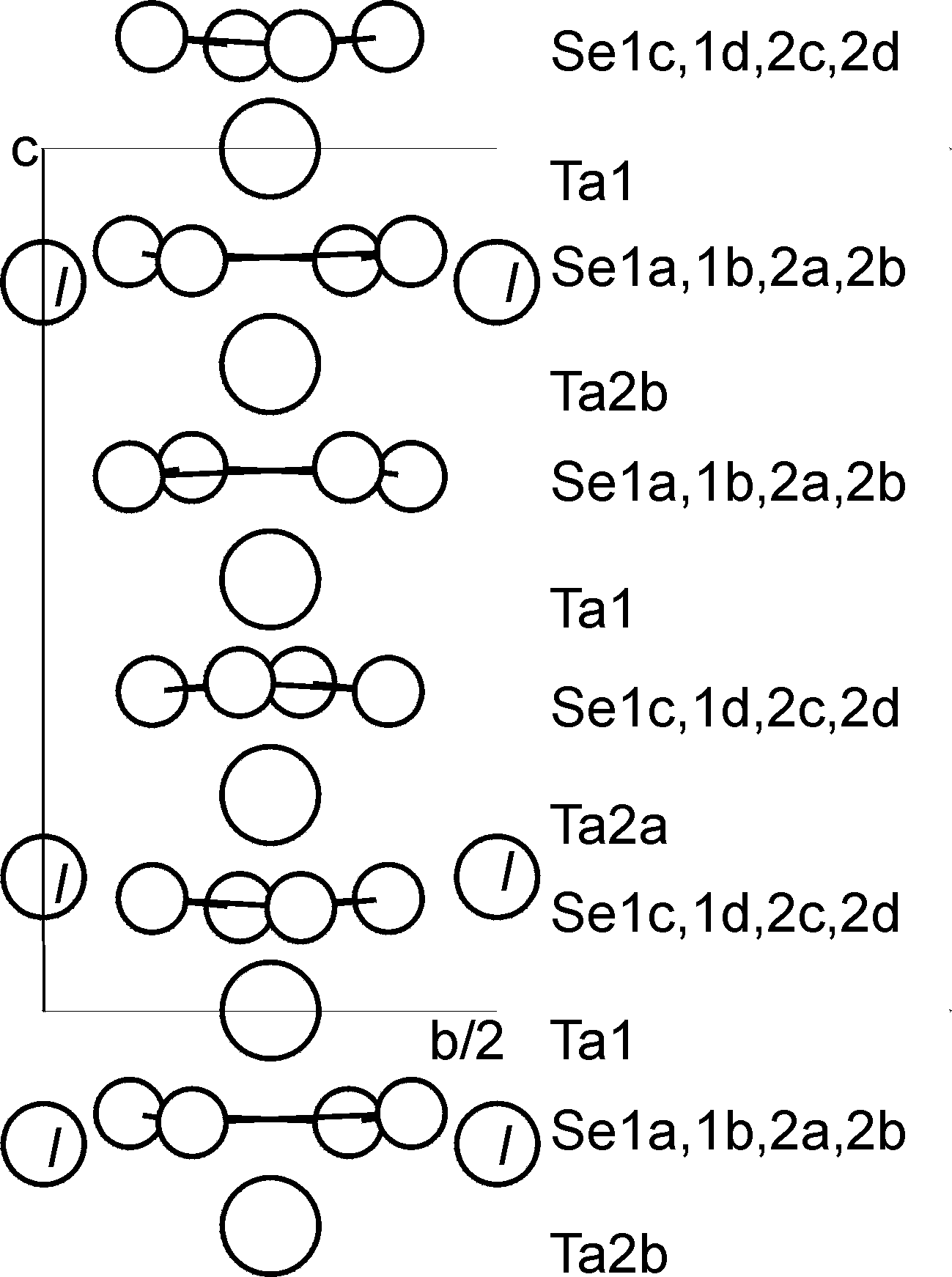
Fig. 2: The structure of the TaSe₄ chain centered on x=y=0.25.

Since about 1983 it has been known that (TaSe₄)₂I has a phase transition at TCDW = 263 K towards a Charge-Density-Wave (CDW) state at low temperatures. However, the crystal structure was not known, which prevented the development of a detailed model about the CDW transition and it prevented an understanding of the physical properties of the CDW state.

In the CDW state each main reflection in the x-ray diffraction is surrounded by eight incommensurate satellites at (± 0.064, ± 0.064, ± 0.151). The integrated intensities of both the main reflections and the satellites were measured by single-crystal x-ray diffraction at T = 120 K, using synchrotron radiation at the Swiss-Norwegian Beam-line BM01 at the European Synchrotron Radiation Facility (ESRF) in Grenoble.

The specific properties of synchrotron radiation were necessary to resolve the main reflections and the surrounding satellites, in order to obtain integrated intensities for each individual reflection. A major question concerning the structure of the CDW was whether the CDW state is a single-domain/multi-q state (tetragonal or orthorhombic symmetry), or a multi-domain/single-q state (monoclinic symmetry). We found that the CDW state comprises of four domains, and it is characterized by one modulation wavevector. The structure has monoclinic symmetry according to the superspace group F2(0, β, γ) with β=0.128 and γ=0.151. In the CDW state the crystal possesses an incommensurately modulated structure, that needs to be described by the (3+1)-dimensional superspace method. Refinements against the measured intensity data resulted in accurate values for the the atomic coordinates.

The positions of the atoms in the the CDW state are described by the atomic coordinates of the basic structure (the structure at room temperature) and a deviation from these basic positions as described by modulation functions. The major part of the modulation is a transverse acoustic wave with approximately equal amplitudes on all atoms of sizes of about 0.13 Å. A modulation of secondary size is found on the Ta atoms with displacements parallel to the 1D chains of magnitudes of 0.025 Å. Displacements of neighboring atoms within on chain are approximately 90° out of phase, and these displacements can be interpreted as representing the CDW on the Ta chains. A Landau Free Energy model was developed, that shows that symmetry arguments allow the phase transition to be second-order.

A cluster model for the CDW state

A more detailed picture of the structure of the CDW state can be obtained from the so-called t-plots of the interatomic distances.
As an example consider the distance between the atoms Ta1 and Se1a (Fig. 2). Neighboring atoms are at a distance of about 2.65 Å, but the precise values are different in each unit cell. All these distances are summarized in an interval [0,1> for t (trace 1 in Fig. 3). Distances on a single curve which are close in t value refer to atom pairs far apart in the structure. However, the curves corresponding to different distances are correlated, and Fig. 3 displays the variation in the distances towards the eight Se atoms in the first coordination sphere of Ta1. It is found that these variations are small, with a total range of about 0.1 Å. The maximum value of the variation of a single contact is even smaller at 0.06 Å. These observations reflect the fact that the short Ta to Se contacts represent chemical bonds, and that these chemical bonds keep their strength in the modulated structure.

The chains of Ta atoms parallel the c-axis support the quasi-1-dimensional (1D) electron bands, with shortest distances between Ta1 and Ta2 in the basic structure. The sequence of Ta atoms along a chain in the monoclinic superstructure is (-Ta1-Ta2b-Ta1-Ta2a-)_∞. In Figure 4 the t-plot is given of the 7 short Ta-Ta distances within two periods along a chain. This plot shows that when two consecutive distances are shorter than average (e.g. the distances numbers 2 and 3 in point A), the neighboring distances (numbers 1 and 4) are longer than average. This means, that in point A a cluster of 3 Ta atoms is formed, that consists of Ta2b-Ta1-Ta2a. Again in point A, the distances 5 and 7 are longer than average, while the distance number 6 has attained the shortest possible value. Thus it is found that for t-values around point A, the chain separates into clusters of 3 Ta atoms, isolated Ta atoms and pairs of Ta atoms. For t-values around the point A' and other A-type points the situation is similar, but the clusters involve different Ta atoms. The points of type B represent transition points between clusters formed between one set of atoms and clusters formed between other atoms.

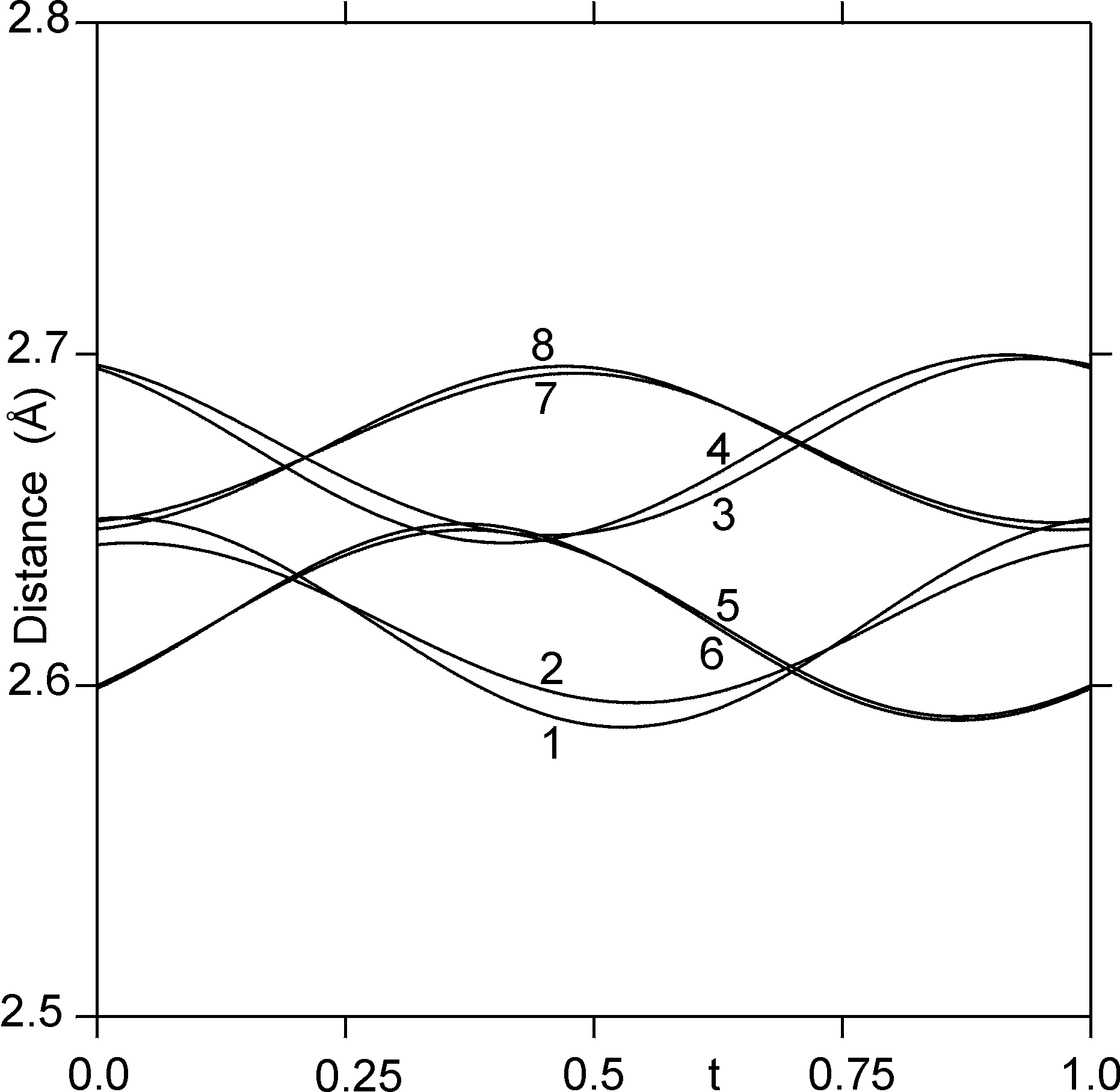
Fig 3.: Interatomic distances between Ta1 and the eight surrounding Se atoms as a function of the fourth superspace coordinate t. The numbers 1 through 8 refer to the distances of Ta1 and the atoms at z~-0.12: Se1a (1), Se1b (2), Se2a (3), Se2b (4), and the atoms at z~ 0.12: Se1c (5), Se1d (6), Se2c (6), Se2d (8).

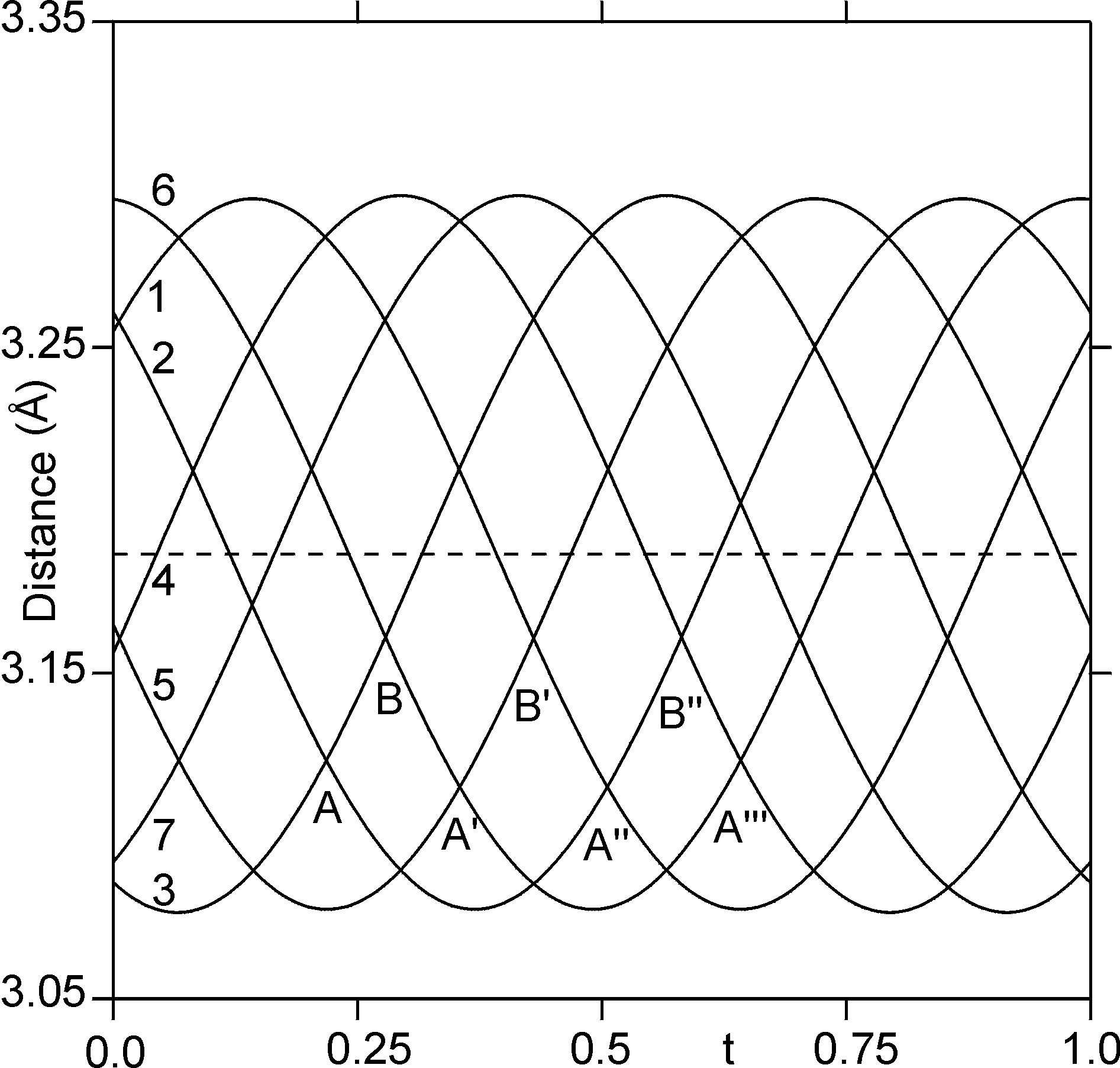
Fig. 4: Interatomic distances between consequetive Ta atoms along a chain as a function of the fourth coordinate t. Shown are the 7 distances along the chain of 8 atoms Ta (z=-0.25)-Ta2b-Ta1-Ta2a-Ta1-Ta2b-Ta1-Ta2a (z=1.5). They are numbered 1 through 7 in this order. Special t-values are denoted by letters A, A',···. The dashed line denotes the average distance of 3.18 Å, which is the same for all atom pairs.

Consideration of all variations in the shortest Ta-Ta contacts thus shows that the superstructure involves the formation of clusters of 3 Ta atoms, the formation of Ta atom pairs and the presence of isolated Ta atoms. This is considered as evidence, that the phase transition represents the formation of a CDW on the chains of Ta atoms. The CDW modulation should not be interpreted as the formation of tetramers, as it was suggested previously.

Conclusions

The modulation in (TaSe₄)₂I is found to split into two parts. The major part of the modulation represents a tranverse acoustic wave, involving displacements of similar magnitudes on all atoms. A modulation of secondary importance is found on the Ta atoms only, with displacements of about 0.025 Å parallel to the directions of the chains. This latter modulation represents the CDW as it is located on the chains of Ta atoms.

The appearance of the large acoustic-like modulation with no apparent relation to the CDW is a peculiar feature of the phase transition, that is not understood yet. Within the theory of quasi-one-dimensional electronic systems one would have expected a modulation wavevector of the form (0,0,γ). The incommensurate transverse component of the modulation wavevector reflects the relative phases of the CDWs on neighboring chains. It might be the result of the interactions between the CDW and the acoustic wave.

Literature

[1] S. van Smaalen, E.J. Lam and J. Lüdecke, J. Phys.: Condens. Matter 13, 9923- 9936 (2001).